今日大綱

• 什麼是純量 (scalar)、向量 (vector)、矩陣 (matrix)與張量 (tensor)
• 矩陣運算

什麼是純量 (scalar)、向量 (vector)、矩陣 (matrix)與張量 (tensor)

純量 (scalar)為常數，通常使用小寫字母斜體表示，如a。

向量 (vector)為一維的張量，具有方向性，通常以小寫斜體粗體表示，如 a。如果想表示向量的第n個元素，將會在右下角的小標加入n。

矩陣 (matrix)維二維的張量，每一列所表示的是每筆資料，而矩陣的每一行所表示的是每個特徵，通常矩陣以大寫斜體粗體表示，如 A。

張量 (tensor)通常表示為二為以上的資料，而深度學習常使用的套件Tensorflow的tensor指的就是張量，訓練模型時將會大量地使用張量學習。

矩陣運算

在做矩陣運算時，需要注意做加減時，兩個矩陣的大小需一致，矩陣大小的表示法為mn，代表有m列n行。下圖為加法的例子，如矩陣大小為22，只能與同樣大小為2*2的矩陣運算，而加法就是將相對應位置的數字相加，減法也是一樣的道理。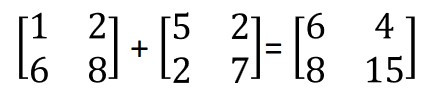

矩陣相乘時，所計算的方式不同於加減法，是使用內積 (dot product)的方式做運算，內積的表示法為一個點。相乘時有一個規則須符合，左邊矩陣的第二個維度需與右邊矩陣的第一個維度相同，例如mk的矩陣與kn的矩陣，而這兩個矩陣相乘將會得到m*n的矩陣。算法如下:

另外，還有一些特殊的矩陣如轉置矩陣 (transpose)，如果23的矩陣轉置將得到32的矩陣，行列互換，表示法在矩陣右上角加上T。

單位矩陣 (identity matrix)為對角線為1，其他的值為0，且為方陣。方陣代表行與列的數目相等。單位矩陣通常以大寫斜體I表示。對角矩陣 (diagonal matrix)則是矩陣為方陣，且上半部與下半部對稱。

最後一個為反矩陣。矩陣A必須為方陣，且為非奇異 (non-singular)方陣，其反矩陣才存在，矩陣A與反矩陣相乘時，將會得到單位矩陣。

結束之前，還有一些小提醒，第一個為矩陣A與矩陣B相乘並不會等於矩陣B乘矩陣A，當位置對調時結果會不一樣。第二個是A的轉置矩陣再次經過轉置後會等於原來的矩陣A。最後一個，矩陣A與它的反矩陣相乘將得到單位矩陣，前提是反矩陣存在。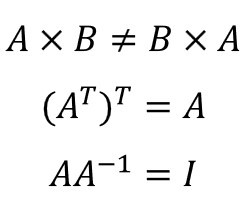

感謝您的瀏覽!